Below the sphere x 2y z2 = 1, using cylindrical or spherical coordinates, whichever seems more appropriate Recall that the centroid is the center of mass of the solid assuming constant density Solution In spherical coordinates, the regions are given by 0 ˚ ˇ=4;0 ˆ 1 Thus, we compute the volume in spherical coordinates Vol(E) = ZZZ EUse spherical coordinates to evaluate the triple integral e−x2−y2−z2 x2y2z2 dV, ∫∫∫ E where E is the region bounded by the spheres x2y2z2=25 and x2y2z2=81 Change to spherical coordinates ρ2=25 ρ2=81 (5 pts) Set up the Integral e−ρ2 ρ ρ2sinφdρdφdθ ρ=5 ∫9 φ=0 ∫π θ=0 ∫2π (5 pts) (5 pts) Evaluate the IntegralExample 5 Find the z coordinate of the center of mass of the solid consisting of the part of the hemisphere z = p 4 x 2 y2 inside the cylinder x y2 = 2x if the density ˆ = 1 Answer Again we try using cylindrical coordinates, this time from the start Note that x2 y2 = 2x is not centered at the origin x y = 2x z = 4 x y 2 2 2 2 x y z
Cylindrical And Spherical Coordinates Calculus Volume 3
X^2+y^2+z^2=1 in spherical coordinates
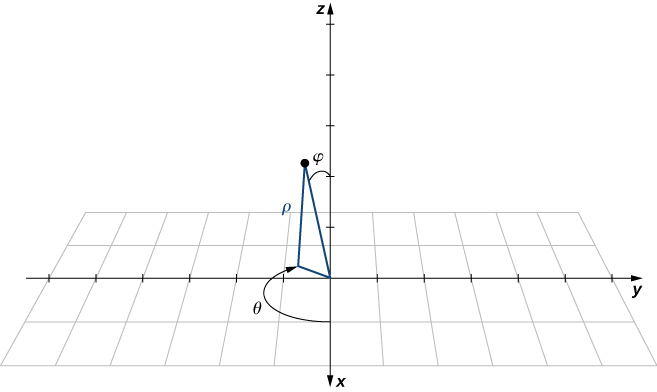
X^2+y^2+z^2=1 in spherical coordinates-Spherical coordinates are somewhat more difficult to understand The small volume we want will be defined by Δρ, Δϕ , and Δθ, as pictured in figure 1561 The small volume is nearly box shaped, with 4 flat sides and two sides formed from bits of concentric spheres When Δρ, Δϕ , and Δθ are all very small, the volume of this little First, we need to recall just how spherical coordinates are defined The following sketch shows the relationship between the Cartesian and spherical coordinate systems Here are the conversion formulas for spherical coordinates x = ρsinφcosθ y = ρsinφsinθ z = ρcosφ x2y2z2 = ρ2 x = ρ sin



Canvas Harvard Edu Files Download Download Frd 1 Verifier Ear7fzwilhy1jf2i9s3glwegihfp2tjxqzv8i0rw
The equation in cylindrical coordinates is Step 2 (b) Conversion from rectangular coordinates to spherical coordinates The equation is Substitute and in above equation The equation in cylindrical coordinates is Solution (a) The equation in spherical coordinates is (b) The equation in spherical coordinates isTranslating Spherical Coordinates to Cartesian Coordinates The next step is to develop a technique for transforming spherical coordinates into Cartesian coordinates, and viceversaWrite the equation in spherical coordinates (a) x2 y2 z2 = 16 (b) x2 − y2 − z2 = 1 Expert Answer 100% (26 ratings) Previous question Next question Get more help from Chegg Solve it with our calculus problem solver and calculator
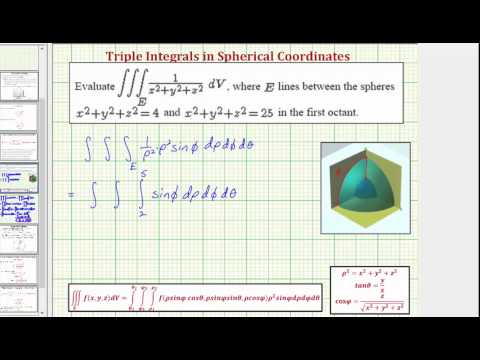
2 (3 pts) Use spherical coordinates to evaluate the triple integral ∫∫∫E xex 2 y2 z2dV where E is the portion of the unit ball x2y2z2≤1 that lies in the first octant 3 (3 pts) Use the spherical coordinates to evaluate the volume of E where E is the solid that lies above the cone z =√x2y2 and below the sphere x2y2z2 =81Angular momentum in spherical coordinates Peter Haggstrom wwwgotohaggstromcom mathsatbondibeach@gmailcom 1 Introduction Angular momentum is a deep property and in courses on quantum mechanics a lot of time is devoted to commutator relationships and spherical harmonics However, manyUse spherical coordinates to find the volume below the sphere x2 y2 z2 = 1 and above the cone z = p x2 y2 Solution R = n (ρ,φ,θ) θ ∈ 0,2π, φ ∈ h 0, π 4 i, ρ ∈ 0,1 o The calculation is simple, the region is a simple section of a sphere V = Z 2π 0 Z π/4 0 Z 1 0 ρ2 sin(φ) dρ dφ dθ, V = hZ 2π 0 dθ ihZ π/4 0
This video explains how to set up a triple integral using spherical coordinates and then evaluate the triple integralhttp//mathispower4ucomUse cylindrical or spherical coordinates, whichever seems more appropriate 35 Find the volume and centroid of the solid E that lies above the cone z = x 2 y 2 and below the sphere x 2 y 2 z 2 = 1This video explains how to convert a rectangular equation (cone) to a spherical equationhttp//mathispower4ucom




Cone Area Spherical Coordinates




1 Point Find The Volume Of The Wedge Shaped Region Figure 1 Contained In The Cylinder X2 Y2 4 And Bounded Above By The Plane Z X And Below By The Xy Plane
Spherical coordinates (r, θ, φ) as commonly used in physics (ISO convention) radial distance r (distance to origin), polar angle θ (angle with respect to polar axis), and azimuthal angle φ (angle of rotation from the initial meridian plane)The symbol ρ is often used instead of rThis spherical coordinates converter/calculator converts the rectangular (or cartesian) coordinates of a unit to its equivalent value in spherical coordinates, according to the formulas shown above Rectangular coordinates are depicted by 3 values, (X, Y, Z) When converted into spherical coordinates, the new values will be depicted as (r, θ, φ)Write the equation in spherical coordinates 9 (a) x 2 y 2 z 2 = 9 (b) x 2 – y 2 – z 2 = 1 Buy Find launch Multivariable Calculus 8th Edition James Stewart Publisher Cengage Learning ISBN Buy Find launch Multivariable Calculus The spherical coordinates of a point are (8, /4, Ch 15 Identify the




Cylindrical Coordinates In Matlab




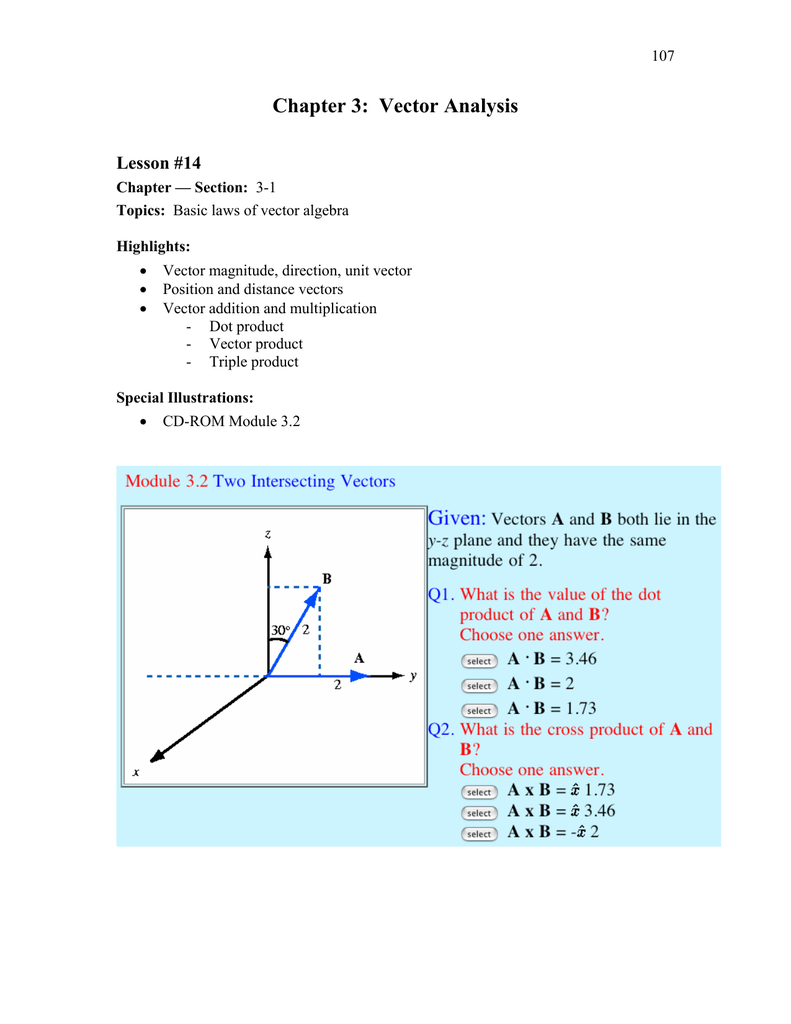
Vectors Answers
Example 1586 Setting up a Triple Integral in Spherical Coordinates Set up an integral for the volume of the region bounded by the cone z = √3(x2 y2) and the hemisphere z = √4 − x2 − y2 (see the figure below) Figure 15 A region bounded below by a cone and above by a hemisphere Solution So, given a point in spherical coordinates the cylindrical coordinates of the point will be, r = ρsinφ θ = θ z = ρcosφ r = ρ sin φ θ = θ z = ρ cos φ Note as well from the Pythagorean theorem we also get, ρ2 = r2 z2 ρ 2 = r 2 z 2 Next, let's find the Cartesian coordinates of the same point The coordinate in the spherical coordinate system is the same as in the cylindrical coordinate system, so surfaces of the form are halfplanes, as before Last, consider surfaces of the form The points on these surfaces are at a fixed angle from the z



12 7 Cylindrical And Spherical Coordinates Mathematics Libretexts



Www3 Nd Edu Taylor Math550 Images Oldexams Exam3a Pdf
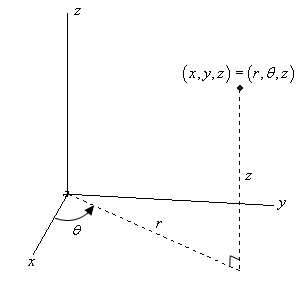
Just as polar coordinates gave us a new way of describing curves in the plane, in this section we will see how cylindrical and spherical coordinates give us new ways of describing surfaces and regions in space † † margin Figure 1471 Illustrating the principles behind cylindrical coordinates Spherical coordinates and finding the boundaries for $\rho$ 1 Given two points on a unit sphere, how to express their angular difference in spherical coordinates?;z), where rand are polar coordinates of the projection of Ponto the xyplane and zis the directed distance from the xyplane to P Figure 1 A point expressed in cylindrical coordinates
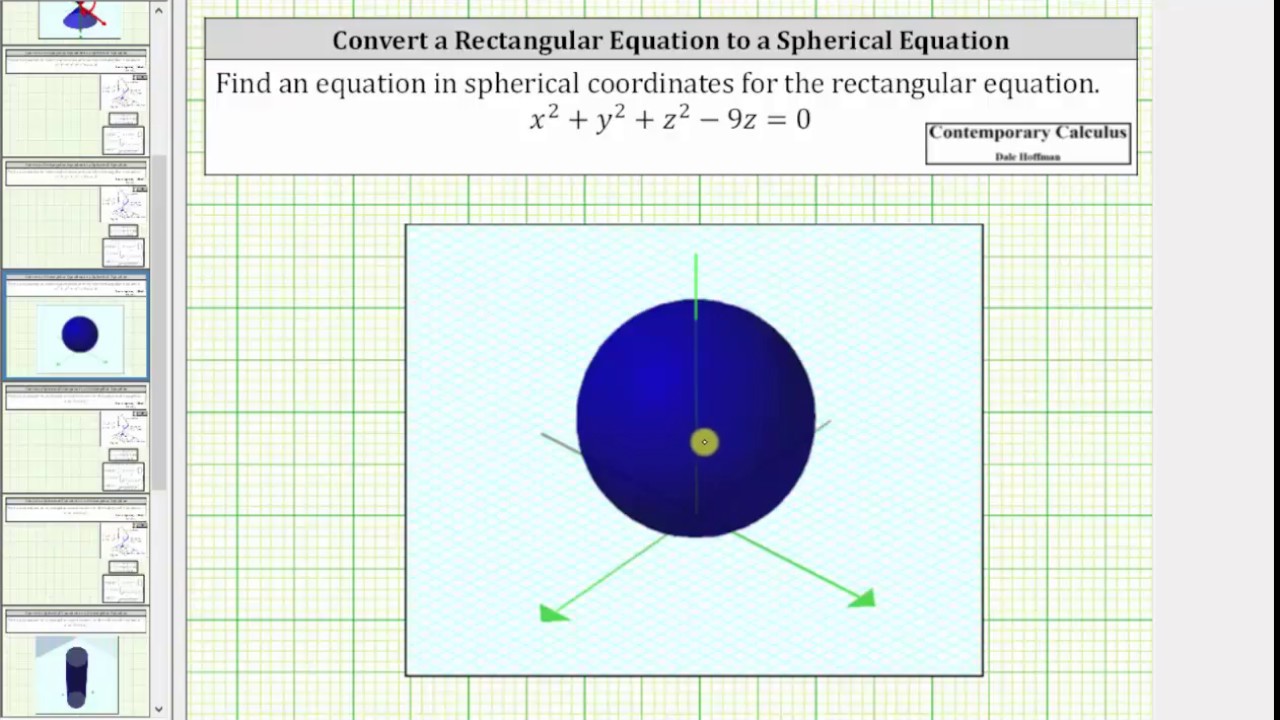



Convert A Rectangular Equation To A Spherical Equation X 2 Y 2 Z 2 9z 0 Youtube



Ocw Mit Edu Resources Res 18 001 Calculus Online Textbook Spring 05 Textbook Mitres 18 001 Strang Pdf
Cartesian Cylindrical Spherical Cylindrical Coordinates x = r cosθ r = √x2 y2 y = r sinθ tan θ = y/x z = z z = z x2 y2 = 25 to cylindrical coordinates b) x2 y2 z2 = 1 to spherical coordinates c) ρ = 2cos φ to cylindrical coordinates 8 EX 4 Make the required change in the given equation (continued) Spherical form r=cos phi csc^2 theta Cylindrical form r=z csc^2theta The conversion formulas, Cartesian to spherical (x, y, z)=r(sin phi cos theta, sin phi sin theta, cos phi), r=sqrt(x^2y^2z^2) Cartesian to cylindrical (x, y, z)=(rho cos theta, rho sin theta, z), rho=sqrt(x^2y^2) Substitutions in x^2y^2=z lead to the forms in the answer Note the nuancesExample 65 Find the spherical equation for the hyperboloid of two sheets x2¡y2¡z2=1 Solution By direct substitution, we obtain, under the standard spherical coordinate system (‰sin`cosµ)2¡(‰sin`sinµ)2¡(‰cos`)2=1 or ‰ 2 ¡ sin`cos2µ¡sin`sin2µ¡cos2` ¢ =1 Example 66 Find a rectangular equation for the surface whose spher



Functions And Variables For Plotting Maxima 5 45 0 Manual




M I T
(Consider using spherical coordinates for the top part and cylindrical coordinates for the bottom part) Verify the answer using the formulas for the volume of a sphere is located inside the sphere x 2 y 2 z 2 = 1, above the x yplane, and inside the circular cone z = x 2 y 2 Eθ is the same angle used to describe the location in cylindrical coordinates;Answer to Write the equation in spherical coordinates x^2y^2z^2=1 By signing up, you'll get thousands of stepbystep solutions to your




Application Of Cylindrical And Spherical Coordinate System In Double




Multiple Integrals H 2 Y Are Continuous Functions On C D And Let F X Y Be A Function Defined On R Then Pdf Free Download
Experts are tested by Chegg as specialists in their subject area We review their content and use your feedback to keep the quality high Transcribed image text Write the equation In spherical coordinates (a) x^2 y^2 z^2 =25 rho = 5 (b) x^2 y^2 z^2 = 1 rho^2 sin^2 (phi) (cos^2 theta sin^2 theta cos^2 (phi)) = 1Cylindrical coordinates are more straightforward to understand than spherical and are similar to the three dimensional Cartesian system (x,y,z) In this case, the orthogonal xy plane is replaced by the polar plane and the vertical zaxis remains the same (see diagram) The conversion between cylindrical and Cartesian systems is the same as for5Determine the bounds (in spherical coordinates) for the following regions between the spheres x 2 y z2 = 1 and x y2 z2 = 4 a)The region between the two spheres and above the xyplane b)The region between the two spheres and to the right of the xzplane




Pdf Ee107 Tutorial 7 Lmsauth fd1efdaad5caefa8a267e8e29b986 Kobinath Rao Academia Edu




64 And 66 Please 64 Describe The Set Of All Chegg Com
Section 17 Cylindrical and Spherical Coordinates Recall that in the plane it is sometimes useful to introduce polar coordinates There are two possible natural and useful generalizations of this to space Cylindrical coordinates (r,θ,z) of a point P(x,y,z) are obtained by usingAnswer to Write the equation in spherical coordinates A) x^2 y^2 z^2 = 81 B) x^2 y^2 z^2 = 1 By signing up, you'll get thousands ofThat zin Cartesian coordinates is the same as ˆcos˚in spherical coordinates, so the function we're integrating is ˆcos˚ The cone z= p x 2 y2 is the same as ˚= ˇ 4 in spherical coordinates (1) The sphere x2y2z = 1 is ˆ= 1 in spherical coordinates So, the solid can be described in spherical coordinates as 0 ˆ 1, 0 ˚ ˇ 4, 0 2ˇ




Evaluate Tribleintegral B E X 2 Y 2 Z 2 Chegg Com




Triple Integral In Spherical Coordinates Ppt Video Online Download
TRIPLE INTEGRALS IN SPHERICAL & CYLINDRICAL COORDINATES Triple Integrals in every Coordinate System feature a unique infinitesimal volume element In Rectangular Coordinates, the volume element, " dV " is a parallelopiped with sides " dx ", " dy ", and " dz " Accordingly, its volume is the product of its three sides, namely dV dx dy= ⋅ ⋅dzSolution We convert the integral to spherical coordinates Change the variables x = ρcosφsinθ, y = ρsinφsinθ, z = ρcosθ, dxdydz = ρ2sinθdρdφdθ The new variables range within the limits 0 ≤ ρ ≤ R, 0 ≤ φ ≤ π 2, 0 ≤ θ ≤ π 2 Then the integral in spherical coordinates becomes I = ∭ U xyzdxdydz = ∭ U Definition spherical coordinate system In the spherical coordinate system, a point P in space (Figure 1279) is represented by the ordered triple (ρ, θ, φ) where ρ (the Greek letter rho) is the distance between P and the origin (ρ ≠ 0);



Triple Integrals In Cylindrical And Spherical Coordinates



Evaluate A Triple Integral Using Spherical Coordinates Triple Integral Of 1 X 2
Section 139 Cylindrical and Spherical Coordinates In the cylindrical coordinate system, a point Pin space is represented by the ordered triple (r; A) Graph the equation using the domain values , and the range values B) Write the equation in spherical coordinates and graph it C) Write the equation in cylindrical coordinates (hint use the factor command outside the simplify command toExample 1762 An object occupies the space inside both the cylinder x 2 y 2 = 1 and the sphere x 2 y 2 z 2 = 4, and has density x 2 at ( x, y, z) Find the total mass Spherical coordinates are somewhat more difficult to understand The small volume we want will be defined by Δ ρ, Δ ϕ , and Δ θ, as pictured in figure 1761



Http Www Math Utah Edu Mmedvin Teaching Math1321 Lecturenotes 13 1321l Vectors Cylindricalandsphericalcoordinates Pdf




Write The Equation In Spherical Coordinates X 2 Chegg Com
Triple Integrals in Spherical Coordinates The spherical coordinates of a point M (x,y,z) are defined to be the three numbers ρ,φ,θ, where θ is the angle of deviation of the radius vector −− → OM from the positive direction of the z axis (Figure 1 ) It's important to take into account that the definition of ρ differs in Spherical Coordinates Solved examples Example 1) Convert the point ( 6, π 4, 2 )from cylindrical coordinates to spherical coordinates equations Solution 1) Now since θ is the same in both the coordinate systems, so we don't have to do anything with that and directly move on to finding ρ ρ = r 2 z 2 = 6 2 = 8 = 2 2(Again, look at each part of the balloon separately, and do not forget to convert the function into spherical coordinates when looking at the top part of the balloon) Now the pilot activates the burner for 10 10 seconds This action affects the temperature in a 12 12footwide column feet high, directly above the burner A cross section




In Spherical Coordinates For The Region X 2 Y 2 Z 2 Geq1 X 2 Y 2 Z 2 Leq4 Z Geq Sqrt X 2 Y 2 Why Does Psi Range From 0 To Pi 2 Mathematics Stack Exchange




List Of Common Coordinate Transformations Wikipedia
X^2y^2z^2=1 WolframAlpha Have a question about using WolframAlpha?Contact Pro Premium Expert Support » Spherical coordinates, also called spherical polar coordinates (Walton 1967, Arfken 1985), are a system of curvilinear coordinates that are natural for describing positions on a sphere or spheroid Define theta to be the azimuthal angle in the xyplane from the xaxis with 0



Canvas Harvard Edu Files Download Download Frd 1 Verifier Ear7fzwilhy1jf2i9s3glwegihfp2tjxqzv8i0rw



2
The hyperlink to Cartesian to Spherical coordinates Bookmarks History Related Calculator Shortest distance between two lines Plane equation given three points Volume of a tetrahedron and a parallelepiped Shortest distance between a point and a plane Cartesian to Spherical coordinatesFind stepbystep solutions and your answer to the following textbook question Use spherical coordinates Evaluate triple integral (x^2y^2)dV, where E lies between the spheres x^2y^2z^2=4 and x^2y^2z^2=9To do the integration, we use spherical coordinates ρ,φ,θ On the surface of the sphere, ρ = a, so the coordinates are just the two angles φ and θ The area element dS is most easily found using the volume element dV = ρ2sinφdρdφdθ = dS ·dρ = area thickness so that dividing by the thickness dρ and setting ρ = a, we get




Application Of Cylindrical And Spherical Coordinate System In Double



3d Integration Cylindrical Coord




Table Of Spherical Harmonics Wikipedia




Finding Volume For Triple Integrals Using Spherical Coordinates Krista King Math Online Math Tutor
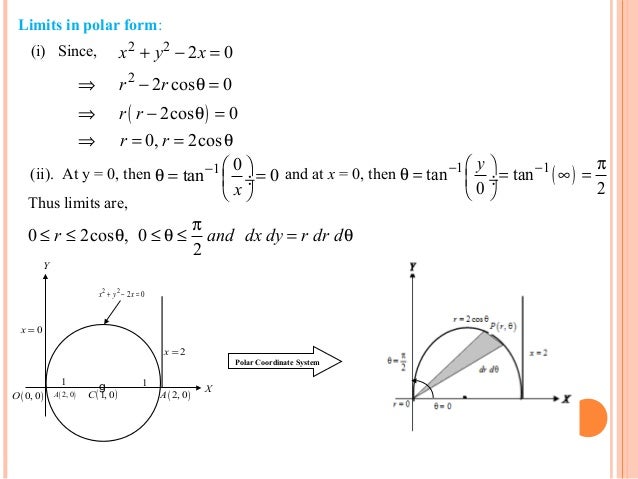



Application Of Cylindrical And Spherical Coordinate System In Double




1 Double Integrals Cankaya Universitesi Flip Ebook Pages 1 16 Anyflip Anyflip
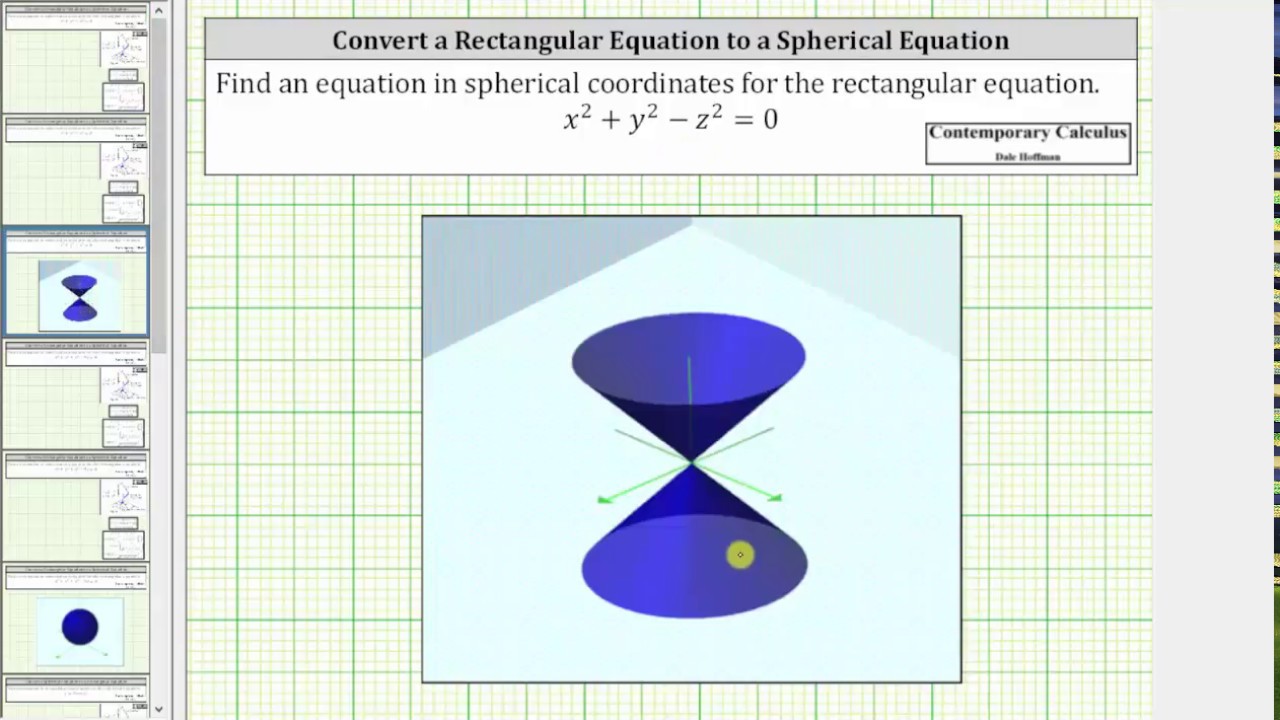



Convert A Rectangular Equation To A Spherical Equation X 2 Y 2 Z 2 0 Youtube
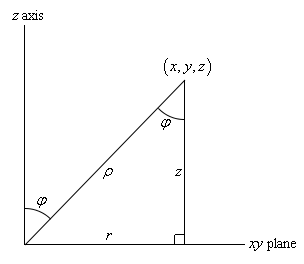



Calculus Iii Spherical Coordinates




Volume Of A Snow Cone In Cylindrical And Spherical Coordinates Youtube



1



Surfaces
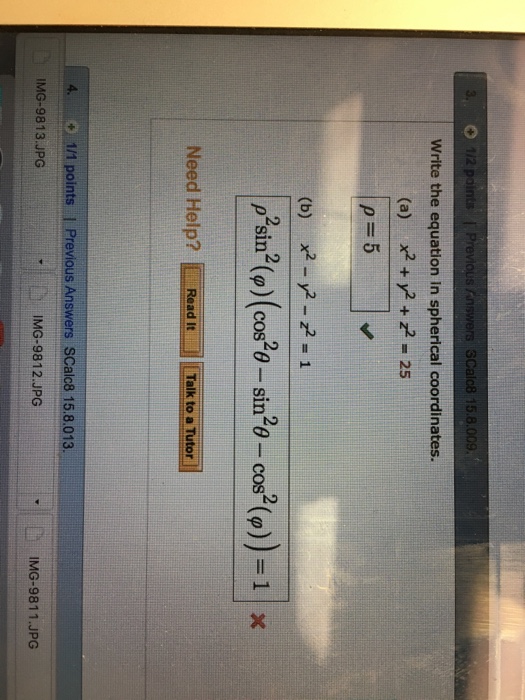



Write The Equation In Spherical Coordinates A X 2 Chegg Com




Answered Q1 Transform The Vector To Cylindrical Bartleby
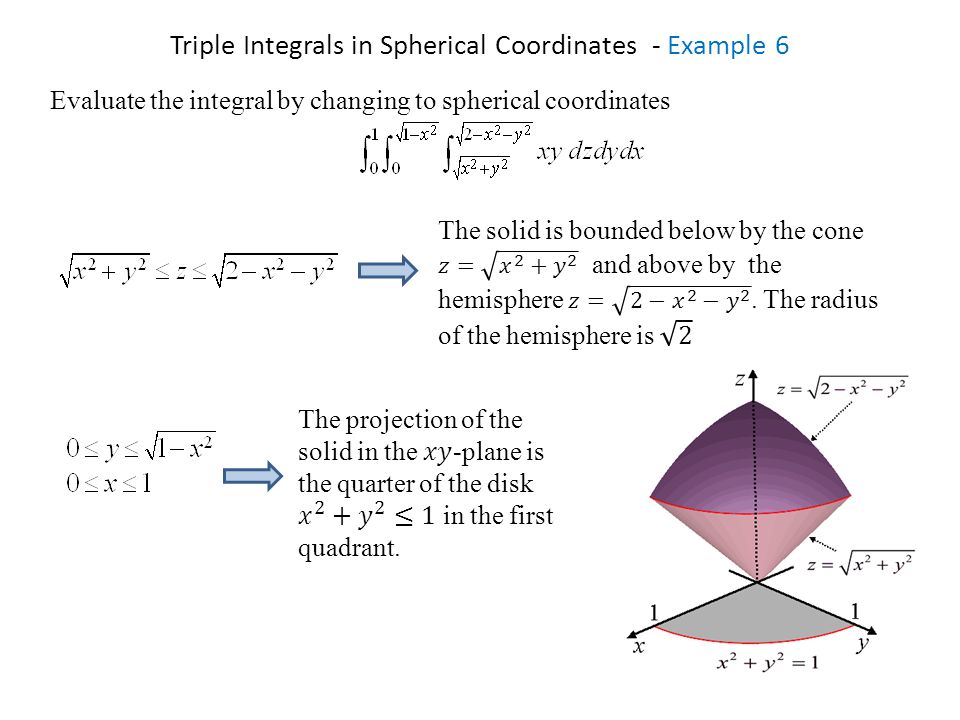



Triple Integral In Spherical Coordinates Ppt Video Online Download




Express The Surface X2 2y2 Z2 1 In Spherical Chegg Com
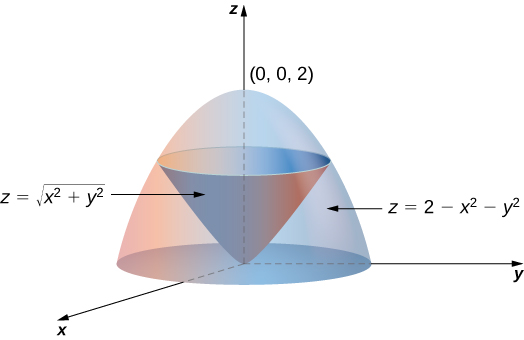



Triple Integrals In Cylindrical And Spherical Coordinates Calculus Volume 3




Triple Integrals In Spherical Coordinates Article Khan Academy



Http Legacy Www Math Harvard Edu Archive 21a Summer 10 Handouts Homework2 Pdf




Describe The Given Set In Spherical Coordinatees 47 Chegg Com




Understanding Integrals With Spherical Coordinates Mathematics Stack Exchange




1 Point Use Spherical Coordinates To Evaluate The Triple Integral Dv E X Y Z E Vx2 Y2 Homeworklib



Cylindrical And Spherical Coordinates Calculus Volume 3




Mat 241 Homework Set 10 Mesa Community College Pages 1 4 Flip Pdf Download Fliphtml5




Regionplot3d In Cylindrical Or Spherical Coordinates Mathematica Stack Exchange




Traniate The Vector و دما 4 To Spherical Coordinates P And Y You Must Have Homeworklib



Evaluate 1 X 2 A 2 Y 2 B 2 X 2 C 2 Dx Dy Dz Over The Ellipsoid X 2 A 2 Y 2 B 2 Z 2 C 2 1 Applied Mathematics 2 Shaalaa Com




Use The Spherical Coordinates To Compute The Integral Int Limits B Z 2 Dx Dy Dz Where B Is Defined By 1 Leq X 2 Y 2 Z 2 Leq 4 Mathematics Stack Exchange



Calculus Iii Cylindrical Coordinates




Copyright C Cengage Learning All Rights Reserved Ppt Download




1 Point Use Spherical Coordinates To Evaluate The Chegg Com




Multiple Integrals H 2 Y Are Continuous Functions On C D And Let F X Y Be A Function Defined On R Then Pdf Free Download




Calc 501 1000 By James Bardo Issuu




Section 12 6 Triple Integrals In Cylindrical Coordinates Ppt Download




Write The Equation 3 Z X 2 Y 2 In Chegg Com




Multiple Integrals H 2 Y Are Continuous Functions On C D And Let F X Y Be A Function Defined On R Then Pdf Free Download




Tut02 Vector Calculus For Engineers Mamf 12 Tutorial 2 1 For Each Of The Following Functions Sketch And Label The Family Of Level Curves Use Course Hero



Www Ualberta Ca Rjia Math215 Hwks Sol5 Pdf




Ex 1 Convert Cartesian Coordinates To Spherical Coordinates Youtube




Thomas Calculus 11e 1263 1564 Pages 151 0 Flip Pdf Download Fliphtml5




Vectors Answers




Vectors And The Geometry Of Space Monografias Com




15 8 Triple Integrals In Spherical Coordinates Mathematics Libretexts



2
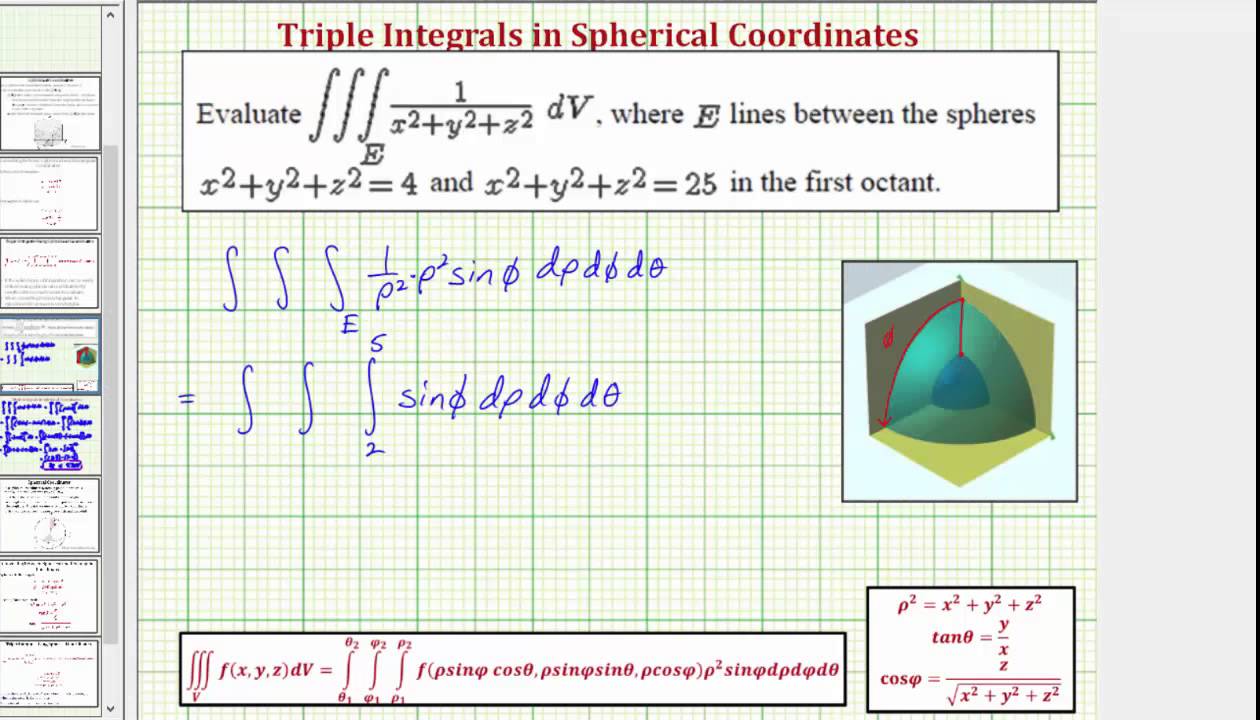



Evaluate A Triple Integral Using Spherical Coordinates Triple Integral Of 1 X 2 Y 2 Z 2 Youtube



2




How To Find The Volume Of An Ellipsoid Quora




Vectors And The Geometry Of Space Monografias Com




Find The Center Of Mass Of The Region X 2 Y 2 Z 2 Less Than Or Equal To1 Z Greater Than Or Equal To 0 Assuming Uniform Density Study Com
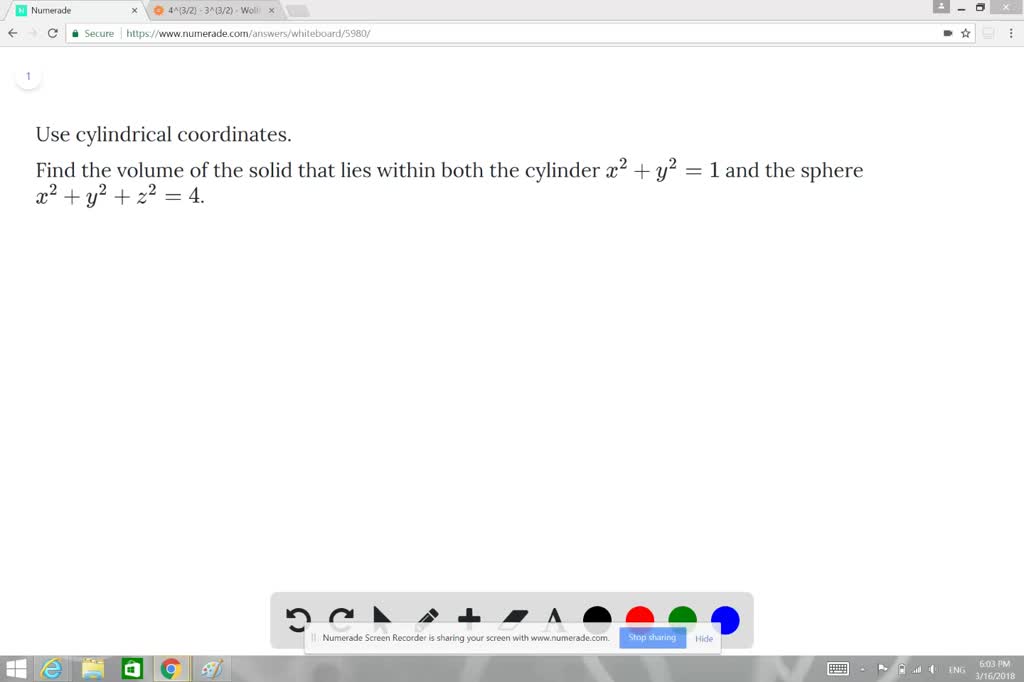



Solved Use Cylindrical Coordinates Find The Volu



1



Search Q Evaluate The Iterated Integral By Converting To Polar Coordinates Tbm Isch




Ppt F X A Function Of A Variable X Powerpoint Presentation Id




Equation Of A Sphere Expii



Ocw Mit Edu Resources Res 18 001 Calculus Online Textbook Spring 05 Textbook Mitres 18 001 Strang Pdf




Solution Manual For Engineering Electromagnetics 8th Edition By Hayt By A Issuu




Mat 21d Lecture 8 Triple Integrals In Cylindrical And Spherical Coordinates Mat 21d Lecture Triple Integrals In Cylindrical And Spherical Coordinates Studocu



The Divergence Theorem



How To Parametrize The Cone Math Z Sqrt X 2 Y 2 Math Where Math Z Math Is Between Math 0 Math And Math 4 Math Inclusive Quora




Engineering Mathematics 233 Solutions Double And Triple Integrals



Www Math Purdue Edu Kyochman Ma261 Notes16 5 Pdf




Use Spherical Coordinates Find The Volume Of The Solid That Lies Within The Sphere X 2 Y 2 Z 2 4 Above The Xy Plane And Below The Following Cone Z Sqrt X 2




Write The Equation In Spherical Coordinates A X2 Chegg Com



1



Solved Use The Cylindrical Coordinates To Find The Volume Of The Solid Above The Paraboloid Z X 2 Y 2 And Inside The Sphere X 2 Y 2 Z 2 Course Hero
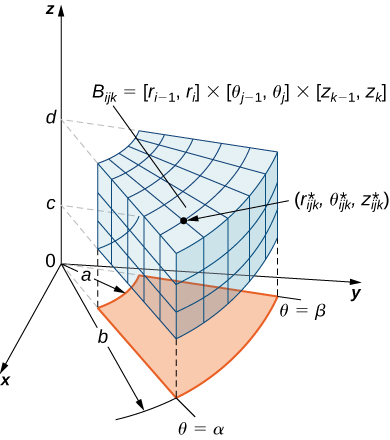



15 8 Triple Integrals In Spherical Coordinates Mathematics Libretexts




Math 21a Midterm I Review




Figure 1 U2 X Y D U 1 X Y Yr X Y Z Dv Xr X Y Z Dv M Yz E Pdf Free Download



Http Www Math Drexel Edu Classes Calculus Resources Math0hw Homework11 8 Ans Pdf




15 8 Triple Integrals In Spherical Coordinates Mathematics Libretexts




User Polar Coordinates To Find The Volume Of The Solid Above The Cone Z Sqrt X 2 Y 2 And Below The Sphere X 2 Y 2 Z 2 1 Homework Help And Answers Slader



Solved A Solid Lies Above The Cone Z Sqrt X 2



Chapter 3 Vector Analysis




Write The Equation In Spherical Coordinates X 2 Chegg Com



Http Pg Gda Pl Static Mathematics Teaching Materials Calculus C E Tripleintegrals Pdf




Answered 6 Match The Integrals With The Type Of Bartleby




Triple Integrals In Spherical And Cylindrical In Rectangular Coordinates Dv Dzdydx In Cylindrical Coordinates Dv R Dzdrd8 In Spherical Coordinates Ppt Download




How Do You Find The Volume Of A Solid Where X 2 Y 2 Z 2 9 Is Bounded In Between The Two Planes Z 2x 2 And Z 2x 3 Socratic



Www Math Uh Edu Bekki 2433 Su16 Notes Sn14 1 Pdf



Http Macs Citadel Edu Zhangli Courses Taught Fall16 Courses Math231 Quiz16 Key Pdf



Calculation Of Volumes Using Triple Integrals Page 2



0 件のコメント:
コメントを投稿